摘要:高溫合金因其良好的材料性能被廣泛的用于各領域,超聲振動輔助磨削已經成為磨削鎳基高溫合金等難加工材料的潛在技術。本文基于橢圓超聲振動輔助磨削(EUVG)運動學分析構建了不同工藝下的磨削形貌仿真模型并計算磨削表面粗糙度,探究超聲振動幅值對EUVG磨削表面加工質量的影響規律。結果表明EUVG具有獨特的磨削表面形貌,能夠實現對于表面紋理的細化以及打斷效果,并明顯的降低磨削表面粗糙度。最后通過單顆粒以及砂帶磨削實驗驗證模型的可靠性。為探索GH4169高溫合金EUVG的高質量加工工藝參數優化提供了理論依據。
1.超聲振動輔助砂帶磨削表面創成分析
磨粒沿著磨粒運動軌跡,對工件進行材料去除以及表面形成。二維超聲振動輔助砂帶磨削相較于一維超聲振動輔助磨削的磨粒軌跡明顯不同并且對工件材料去除、磨削表面形貌與粗糙度等都造成一定影響,本章對磨粒進行了運動學分析、建立了磨粒以及砂帶的數學模型并進行了表面形貌的仿真。為簡化分析過程,在對于EUVG表面形貌進行建模仿真時做出如下假設:(1)砂帶磨削過程中運動穩定;(2)磨削過程中磨粒不發生脫落與磨損;(3)超聲振動在磨削過程中狀態保持穩定。
1.2超聲振動輔助砂帶磨削下表面形貌仿真
本文假設砂帶表面磨粒分布均勻,則磨粒之間的間隔距離?可表示為:
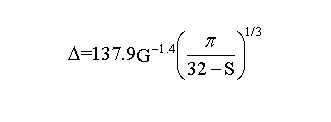
其中G表示磨粒數,S表示結構數(在本文中G=80,S=2)。
磨粒的中心點坐標為G(x0,y0,z0),則磨粒的輪廓表示為:
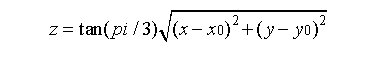
磨粒的平均高度可表示為[28][29]:
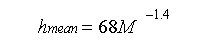
其中M為砂帶粒數。
砂帶磨粒中心的坐標為V(x,y,z),圓錐體的中心點的坐標為G0(x0,y0,z0),則
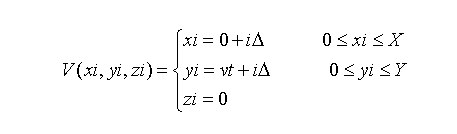
其中X和Y分別為磨削表面在x和y方向的大小,?為兩點之間的間隔距離。
考慮砂帶的彈性磨削特點,由磨粒運動軌跡我們可得知圓錐體的中心點G0(x0,y0,z0)的表達式為:
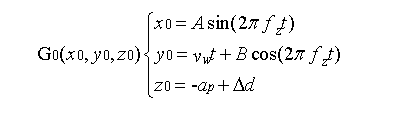
?d為砂帶磨削過程彈性磨削的位移,其中?d≤σm·π(a_p)^2 (tan(θ/2))^2,σm為材料的流動壓力:
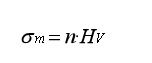
其中HV是材料維氏硬度,n是與工件之間的相互作用,通常n=1.08。
第i顆磨粒的中心的的表達式為:
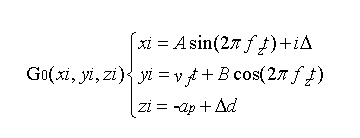
即圓錐體的中心點沿磨粒磨削軌跡運動并對工件表面產生材料去除,Z為圓錐體在工件表面加工后的輪廓值,選取在該空間磨粒輪廓的最小值作為磨削表面的輪廓H可表達為,
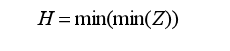
2.1 仿真結果分析
圖2.1所示為不同振幅下使用MATLAB仿真的表面形貌。由于磨削軌跡重復率隨著軸向振幅A和切向振幅B的增加而提高,因此磨削后殘余面積的高度會降低,且能夠提高表面粗糙度和光潔度。
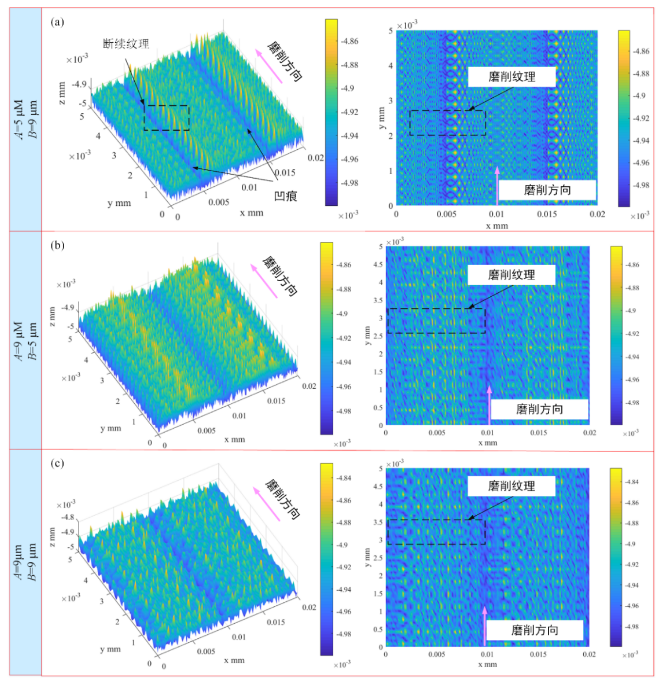
圖2.1不同振幅對于表面形貌的影響(vf=5 mm/s)
3.結論
(1)使用MATLAB對橢圓超聲振動磨削表面形貌進行仿真分析,并通過實驗驗證模型的可靠性。
(2)隨著軸向振幅A的增加,磨削紋理的打斷效果更佳,表面粗糙度降低。切向振幅B的增加對表面形貌的影響主要表現為,重復磨削區域增加,磨削表面光潔度有所提高,表面粗糙度減小。但對紋理特征并沒有明顯的影響。


 手機資訊
手機資訊 官方微信
官方微信








 豫公網安備41019702003604號
豫公網安備41019702003604號