砂帶磨削是砂帶這一特殊形式的磨削工具，借助于張緊機構使之張緊，和驅動輪使之高速運動，并在一定壓力作用下，使砂帶與工件表面接觸以實現磨削加工的整個過程。

       砂帶磨削是木質材料加工技術中尤為重要的一項。砂光機占木材加工設備總數的4％左右，而磨削加工占木質材料切削加工的30％左右，磨削能耗占總加工能耗的15％ ～25％。

       磨削的主要目的是定厚（尺寸校準）、去除人造板表面的預固化層等，對木質材料產品的加工精度、表面質量和膠合質量具有至關重要的作用。

       目前關于木質材料磨削加工的理論不足，磨削工藝參數和動力配置不合理，從而導致磨削加工能耗高、產品質量差及磨削機械設計不合理等問題，急需木質材料磨削加工理論研究指導實際磨削生產，以提高材料利用率和產品質量，降低生產能耗。

       磨削參數及木材性質都影響磨削力和磨削功率，且木材砂帶磨削過程的變異性較大。用常規回歸分析法建立經驗模型較為困難，適用范圍較窄，需要建立廣泛適用的數據模型。

       磨削加工包括滑擦、耕犁和切削3個過程。當工件上的壓力非常小時，磨粒只會擦拭工件表面；當壓力略有增加，砂帶磨削開始耕犁和切削木制品表面。滑擦、耕犁和切削的比例反映了單位面積砂帶參與磨削磨粒的量，不同的比例也會導致磨削能耗發生變化。可以通過合理配置磨削參數，增加磨削過程中有效切削的比重。但在實際生產中，切削階段只能通過間接的方式測定。磨削力是磨削加工中最基本的輸出信號，幾乎影響所有磨削現象。

       本研究從磨削力做功出發，采用磨削功率利用率μ（即磨削力做功功率Pst占整個磨削功率Ps的百分比）來間接反映磨削能耗利用效率。

       磨削力包括滑擦、耕犁和切削階段所產生的力，所以磨削力做功基本可以體現磨削過程中材料的彈塑性變形以及切除材料的耗能。若磨削功率利用率大，則可間接說明磨削力做功主要作用于切削階段，即產生材料切除，而滑擦與耕犁階段的磨削熱占總能耗的比例小；若磨削功率利用率小，則可間接說明磨削力做功主要作用于滑擦和耕犁階段，即磨削熱和空氣阻力、噪聲等其他能耗占總能耗的比例大。

       綜上，北京林業大學應俊華，羅斌等重點研究不同磨削工藝參數對實際材料去除效率的影響，體現為磨削力做功在整個磨削能耗中的占比，從而優化磨削工藝參數，指導實際生產，提升能源利用效率。

       1 材料與方法

       1.1　試驗材料

       1.2　試驗方法

       1.3　測試方法

       2 結果與分析

       2.1　砂帶磨削參數對砂光機空轉功率的影響

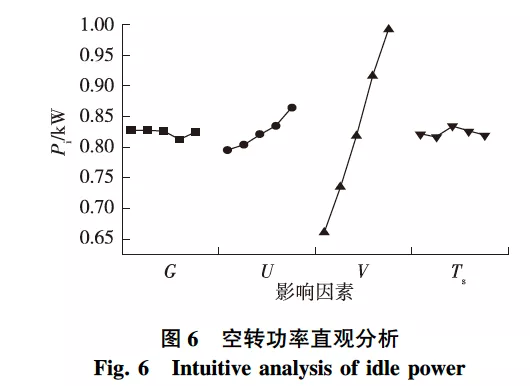
       對影響砂光機在空轉時有功功率（以下簡稱為空轉功率）的磨削參數進行方差分析可知，各參數對空轉功率的影響順序為V＞U＞Ts＞G，砂帶速度和進給速度對空轉功率有高度顯著影響，而砂帶磨料粒度和磨削深度與空轉功率的相關性不大。對空轉功率的直觀分析見圖6。由圖6可知，空轉功率隨著砂帶速度和進給速度的增加基本呈線性增加，且增加最明顯的是砂帶速度。改變砂帶速度和進給速度時，空轉功率的水平極差分別為0.331和0.069kW，水平極差之比約為5。空轉功率的變化規律反映了試驗所用砂光機的部件電機能耗，即砂帶轉動電機功率大于試件進給電機功率。此外，砂帶速度對空轉功率的影響較大也與其引起的風阻較大有關，砂帶轉動時受到的空氣阻力（f）滿足空氣阻力公式：

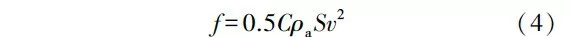
       式中：C是阻力系數，Pa是空氣密度，S是物體有效橫截面積，v是物體移動速度，此處與砂帶速度相同。由式（4）可知，空氣阻力與砂帶速度呈二次方的關系，砂帶速度越大，受到的空氣阻力越大，能量損耗越大。而磨料粒度和磨削深度對空轉功率無影響，側面反映了試驗結果的穩定性和可靠性。

       2.2　砂帶磨削參數對楊木和紅松Psf和μ的影響

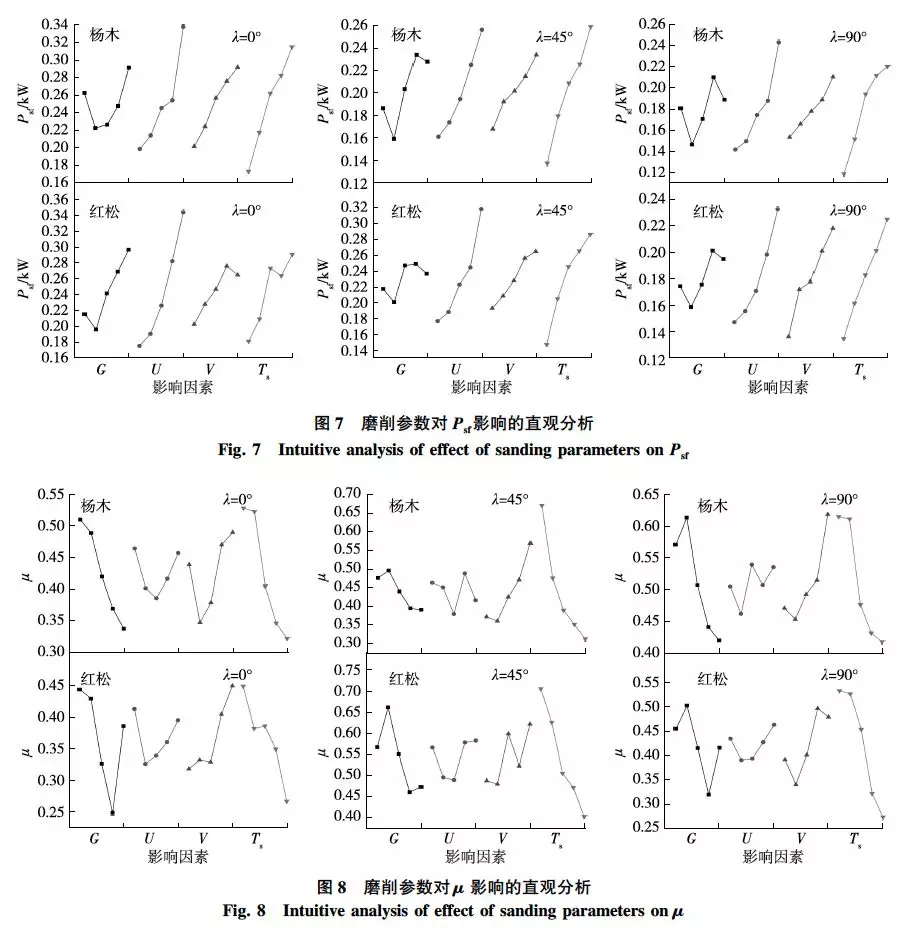
       砂帶磨削參數對楊木和紅松Psf和μ的影響正交試驗方差分析見表2。由表2可知，4個因素都是高度顯著影響Psf的因素，順序為U＞Ts＞V＞G。磨削參數對μ影響的大小順序為Ts＞G＞V＞U，其中，G和V為顯著影響因素，提高砂帶磨削木質材料的功率利用率，主要從改變Ts、G和V的大小出發。Ts和G對Psf和μ均為高度顯著影響，這反映了砂帶磨削木質材料的影響規律，隨著Ts的增加，磨削總量增加，每齒切削量增加，磨削力增大，磨削力做功功率增大。而G可反映磨料粒度和磨粒數目，直接影響每齒切削量，進而影響磨削力，對整個磨削過程的磨削力做功功率產生高度顯著影響。磨削參數U和V都是Psf的高度顯著影響因素，且僅改變U，對Psf影響最大；此外，U可以影響單位時間內磨削木質材料的長度，改變U就可改變單位時間內的磨削量，影響磨粒每齒切削量，進而影響磨削力和Psf的大小。根據式（1），V的增大會導致Psf增大， 但是V的增大也會使單位時間內磨削木材的總磨粒增多，參與切削的磨粒數目增加，每齒切削量減少，磨削力減小，從而使Psf值減小。因此，V對Psf的影響小于U。

       順紋磨削時，Ps和G是影響μ的主要因素，V和U則對μ幾乎沒有影響。楊木順紋磨削時，Ts是μ的高度顯著影響因素；而紅松順紋磨削時，Ts的F值只是接近顯著影響因素。斜紋磨削時，楊木斜紋的不同磨削參數F值大多比紅松斜紋磨削時大。楊木斜紋磨削時，Ts和V是高度顯著影響因素，G和U是顯著因素；紅松斜紋磨削時，Ts和G是高度顯著影響因素，V是顯著因素，U對μ無影響。橫紋磨削時，2種木材的Ts都為高度顯著影響因素；楊木的G為顯著影響因素，紅松的G則對μ無影響；紅松與楊木相比，改變磨削參數U和V時，紅松對μ的影響更小。μ在楊木順紋、斜紋和橫紋磨削時得到的總數據中的極差分別為0.148，0.195和0.158；在紅松順紋、斜紋和橫紋磨削時分別為0.149，0.183和0.168。因此，改變磨削參數時，μ的總改變量從大到小依次為楊木斜紋、紅松斜紋、紅松橫紋、楊木橫紋、紅松順紋、楊木順紋。對于同種木材，μ值的變化量：斜紋＞橫紋＞順紋。楊木磨削時，μ的改變量略大于紅松。紅松的密度和表面硬度都比楊木大，且紋理排列更單一，同種磨削參數磨削時，硬度和密度更小的木材μ 值的變化量更大。磨削參數對Psf影響的直觀分析圖見圖7。由圖7可知，Psf的值隨各參數值的增大而增大。G對Psf值的影響，除順紋磨削時僅有60目1個拐點；斜紋及橫紋磨削時分別在60和100目都有2個拐點。隨著U的增大，Psf逐漸增大，且增大的速度也逐漸增加。隨著磨削參數V和Ts的增加，Psf基本呈直線增大。在不同紋理時的最大值不同，楊木順紋、斜紋和橫紋磨削時的Psf最大值分別為0.34，0.26和0.24kW；紅松順紋、斜紋和橫紋磨削時的Psf最大值分別為0.35，0.32和0.23kW。磨削力做功功率大小順序為順紋、斜紋、橫紋。磨削參數對μ影響的直觀分析見圖8。由圖8可知，隨著磨削參數Ts的增加，μ呈下降趨勢；Ｇ增大時，μ的值也基本呈下降趨勢，斜紋和橫紋磨削時，在60和100目處有2個拐點，紅松順紋磨削時僅有100目1個拐點，楊木順紋磨削時則無拐點；磨削參數Ｕ增加時，μ呈先減小后增大的凹形；磨削參數Ｖ增加時，μ基本呈上升趨勢。這表明順紋磨削時，采用40目砂帶更有利于提高磨削功率的利用率，而斜紋和橫紋磨削時采用60目砂帶更優。采用高速磨削可提高磨削功率的利用率，使用最高進給速度或最低進給速度可稍微提高μ值；在同樣的磨削條件下，隨著Ts的增加，μ在整體上呈降低趨勢，Ts越大，實際磨削深度與設定厚度偏差越大。此外，磨削不同的樹種，在不同紋理方向下，最高磨削效率都不相同。根據各紋理方向下的μ數據匯總，楊木順紋、斜紋和橫紋磨削時的μ平均值分別為0.425，0.442和0.510，紅松順紋、斜紋和橫紋磨削時的μ平均值分別為0.366，0.542和0.420。磨削效率的高低順序為紅松斜紋、楊木橫紋、楊木斜紋、楊木順紋、紅松橫紋、紅松順紋。楊木磨削效率順序（橫紋＞斜紋＞順紋） 與前人研究結果相同，而紅松則為斜紋＞橫紋＞順紋。紅松斜紋磨削效率更高，這是因為針葉材的紋理相比楊木這類闊葉材更通直。對各磨削參數下μ的直觀分析，可得最佳功率利用率（高磨削效率）的磨削方案為：磨削深度0.1mm，砂帶速度10.74m/s，進給速度5.16m/min，磨料粒度60目，楊木橫紋磨削，紅松斜紋磨削。經計算，平均功率利用率45％，最大功率利用率78％，最小功率利用率21％。

       2.3　楊木砂帶磨削參數的BP（back propagation）神經網絡建模　　

       本研究采用單隱層的BP神經網絡系統對楊木的紋理、磨削參數與Psf和μ2種表征量之間的非線性關系建立仿真模型，該中間層神經元數目（隱層節點數）可以根據kolmogorov定理選擇：

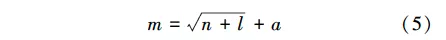
       式中：m是隱層節點數；n是輸入節點數；l是輸出節點數；a是1～10間的常數。具有單隱層的BP神經網絡可以映射所有連續函數，只有當學習不連續函數時才需要2個隱層。因此，本試驗選用單隱層的BP神經網絡。增加隱層節點數，網絡從樣本中獲得信息的能力會有所提高；但如果隱層節點數過多，網絡又可能把樣本中非規律性的內容（如噪聲）記牢，反而降低了泛化能力，也會使訓練時間增加。當樣本數固定時，較少的隱層節點數可能無法表達所有的樣本規律。當樣本數目過少時，有較多隱層節點數的神經網絡得不到有效訓練。經過反復測試，本試驗的隱層最終選用3節點。輸入層（Ｇ、Ｕ、Ｖ、Ts和λ）是五維的向量，所以輸入層為五節點。輸出2個結果（Psf和μ）為二維，所以輸出層為兩節點。BP神經網絡的基本架構和調用函數通過以下代碼完成：

       其中，“threshold”規定輸入向量的最小值（0）和最大值（1），“tansig” 為網絡中間層傳遞函數tansig（），輸出層傳遞函數為對數函數logsig（），訓練函數為trainlm（）。木質材料磨削過程影響結果比較復雜，適當增加訓練次數和減小學習速率，可以提高訓練準確度。網絡訓練次數設置為1000次，學習速率設置為0.01，訓練目標誤差為0.001（0.1％），訓練代碼如下：

       將歸一化后的試驗參數和結果輸入到代碼中，得到訓練代碼并訓練。進行BP神經網絡預測，然后繪制預報誤差曲線，訓練代碼如下：

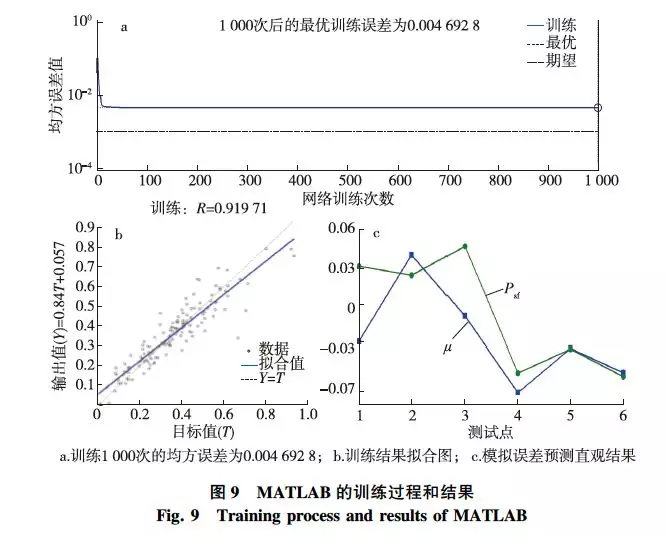
       BP神經網絡的模擬結果見圖9。由圖9a可知，設置期望誤差為0.001，實際1000次訓練后可得均方誤差為0.004 692 8；圖9b顯示了神經網絡輸出值與目標值（T）之間的擬合結果，可知：擬合結果的置信度約為92％，可以滿足預測的基本要求；圖9c為預測時網絡輸出結果與原數據的模擬誤差值，可以看出，最大誤差約為7％。

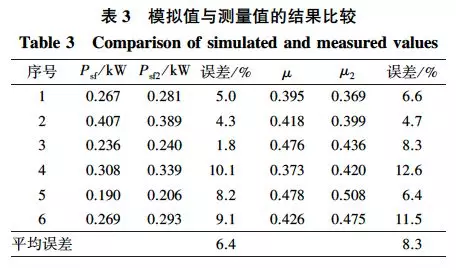
       模擬值與測量值的結果比較見表３。表３ 中Psf和μ表示測量值，Psf２和μ２表示模擬值。Psf的最大相對誤差為10.1％，平均誤差為6.4％；μ的最大相對誤差為12.6％，平均誤差為8.3％，完全可以滿足砂帶磨削楊木時Psf和μ的預測需要。本次預測時間小于2s，因此，BP神經網絡系統減少了分析計算時間。由于木材材質本身的各向異性和多孔性，磨削結果跟金屬等材料有很大區別，木材磨削中有測量結果誤差大和數據噪聲大等缺點，因此，建立Psf和μ的理論與經驗模型較難。而BP神經網絡具有良好的非線性映射能力、泛化能力和容錯能力，可以滿足木質材料磨削的實際建模和預測。

       結 論

       １）磨削參數對Psf的影響順序為Ｕ＞Ts＞Ｖ＞Ｇ，且都為高度顯著影響因素，對μ的影響順序為Ts＞Ｇ＞Ｖ＞Ｕ，Ts為高度顯著影響因素，G和V為顯著影響因素。因此，提高砂帶磨削木質材料的功率利用率，主要考慮改變Ts、G和V3個磨削參數。

       ２）Ts和G是影響Psf和μ的高度顯著影響因素，Ts的影響最大，G次之。木材紋理對μ的影響，楊木磨削時從大到小依次為橫紋、斜紋、順紋，而紅松則為斜紋、橫紋、順紋。

       ３）最佳功率利用率（高磨削效率）的磨削方案為：磨削深度0.1mm，砂帶速度10.74m/s，進給速度5.16m/min，磨料粒度60 目，楊木橫紋磨削，紅松斜紋磨削。平均功率利用率45％，最大功率利用率78％，最小功率利用率21％。

       ４）采用BP神經網絡建立楊木的Psf和μ仿真模型，擬合結果的置信度約為92％，實際預測中Psf的平均誤差為6.4％，μ的平均誤差為8/3％，可以滿足預測的基本要求。

       該文發表于《林業工程學報》2019年第3期。